Subscribe to EThermo
熱流体とは
「熱流体」という言葉と初めて出会ったのは、11年前に日本にある精密機械の大手メーカーのR&D部門に訪問研究インターンをやってきた、まだ大学院の学生の時だった。横浜みなとみらいのオフィスに入った初日に、当時の上司に「熱流体シミュレーションをやってごらん」と誘われた。え~、熱は熱ってわかる、流体は流体ってわかる、「熱流体」って何?、もしかしたら「熱くて流れている物体」、であれば「マグマ!」とバカ発想していた。上司はオフィスの一角に静かに座っている複合機に導いて、印刷ボータンを押して、複合機は一気にガチャンガチャンと動いていた。上司はある樹脂グリルに指差して、「触ってみ?」、私は手首を近付けると、落ち着いた風が吹いているとわかった、手首は徐々に熱くなり、「あっちっちい」、と「熱流体」を初めて感じた。
日本の大学、産業界では「熱流体」という言葉は馴染んでいたが、実は外国では対応している言葉はあまり存在していない。Google翻訳ではThermal Fluidとできるが、英語圏ではとても不自然な表現になる。この言葉こそ、日本語の凄さを示していると思っている。「熱流体」という言葉こそ、熱と流体の深い関係を表現できている。この言葉は、日本人は誰よりも熱と流体のことをよく理解している矢印だと思ってる。
熱と流体は夫婦みたいで、ほとんどの場合は一緒にいる、いろいろな素晴らしい機能を生み出しているし、ただ喧嘩した場合はいろいろな望ましくない不具合も起こしている。先の複合機の例とすれば、トナーを紙に印字する際に、200℃程度の定着器から熱をもらっている。連続して印刷すると、複合機の温度が徐々に上がり、内蔵している複数の小さな扇風機を回して、あちこちに風を吹いて熱を吸引して外に排出している。それで、グリルからは暖かい温風が出ていた。一方、大きい熱量を持っている風は間違えて、感光体や現像機やトナーボックスやROSなど熱に弱い部位に吹き続けると、印字された画像がゆがんだり、トナーが溶融して汚れたりすることができてしまう。または、温度が高い部位に風が吹きついてないと、その部位の温度が高まって、最終的に熱暴走してしまうこともあり得る。
「熱流体」とは、熱量を持つまたは持たせた流体に着眼して、流体と固体の伝熱または温度を十分に考慮することだ
と考えていた。
モノづくりといえば、人間に作られた製品は正しく機能するために、ある幅をもって製品の温度を守る必要がある。ある意味で、人間の体と似ている。製品の温度を守るために、熱流体が登場する。リチウムイオン電池を例とすれば、寒いときには熱風または暖かい水を流して電池を温める。熱いと時には冷風または冷たい水を流して電池を冷やしている。製品を形にしているいろんな形態と機能を持っている固体の温度をケアするためには、気体または液体を駆使してその固体と意図的に熱交換させることが我々人類の知恵だ。手には10本の指を持っているから、だれでも自然的に10進法を身に着けることと同じだ。我々が生きている地球には、陸上では空気が溢れているし、海洋には水が溢れている、人間はずっと”熱流体”に包まれているのだ。
熱と流体の違い
熱流体解析が登場する前に、はるか前から熱解析と流体解析が存在していた。だから、もともと熱解析と流体解析が別々だった。熱解析の支配方程式はフーリエの法則から導いた3次元非定常熱伝導方程式であり、数学的に閉じているものだったため、固体温度の時間空間的な変化を完全に描いている。一方、流体解析の支配方程式はナビエストークス(方程式)であり、時間空間的な乱れの未知の項目があるため、数学的には非完全に閉じていないため、流体の時間空間的な変化を完全に描けていない。
3次元熱伝導方程式: $$ \nabla^{2}T-\frac{1}{k}\frac{\partial T}{\partial t}=-\frac{\dot{q}}{K}$$
どんなに複雑な固体伝熱問題でも必ず上記方程式に従っている、熱伝導に関してのすべてはこのシンプルな数式で完全に描いている、これは数学な魅力だろうね。
数式の中にできている常数Kは物体の熱伝導率、kは物体の熱拡散率。Kとkとも空間座標と伴って変化はしない、物性によって決まれているから。Kとkとも温度依存性があるが、多くは温度に対して激しく変化しないため、常温範囲であれば、Kとkは定数として扱える。そうすると、上記数式は温度の時間偏微分と空間偏微分しか残っていなく、非線形要素が含まれていない。変数分離やラプラス変換の数学手法を用いては、上記数式を線形化処理が可能になり、理論解を得ることができる。理論解が得るものは、だいたいおろしい怪物ではない。比較として、ナビエストークス方程式ではごく限られた層流シナリオで理論解があり、ほとんどの三次元流体問題は理論解が存在しないし、乱流を考慮すると厳密な数式さえ存在しない、流体運動はほんとにまた倒されていない大モンスターだ。ある意味で、熱屋は流体屋よりは神様に恵まれているほうだ。アインシュタインさんは若いごろ乱流問題をやってみたが直ちに諦めた、人類はまだそのモンスターを倒せる力を持っていないと言った説もある。
さて、ナビエストークス方程式をもう一回見てみよう。
$$ \frac{\partial \mathbf{u}}{\partial t}+(\mathbf{u} \cdot \nabla ) \mathbf{u} = -\frac{\nabla{P}}{\rho}+\nu \nabla^2 \mathbf{u}+\frac{\mathbf{F}}{\rho}$$
なるほどという感じだよね、左第2項は速度ベクトルとナブラ演算子の点乗積からできた新しい演算子を速度ベクトルに働いてできた非線形的な移流項となり、線形処理はできなくなる。
また理解しづらいかもしれないため、一緒に思考試験やってみてください。ある瞬間に、2次元空間のある1点に、質量ない赤い風船を置けたことを想像してみよう。風船はその空間の流れ場に沿って移動されるね、置かれた瞬間の速度はその空間の流れ場の速度と同じだ。では、微小な時間間隔\( \Delta t \)後の次の瞬間の風船の速度はどうなるか、下図のように考えて、第一原理から数学的に導くことができる。
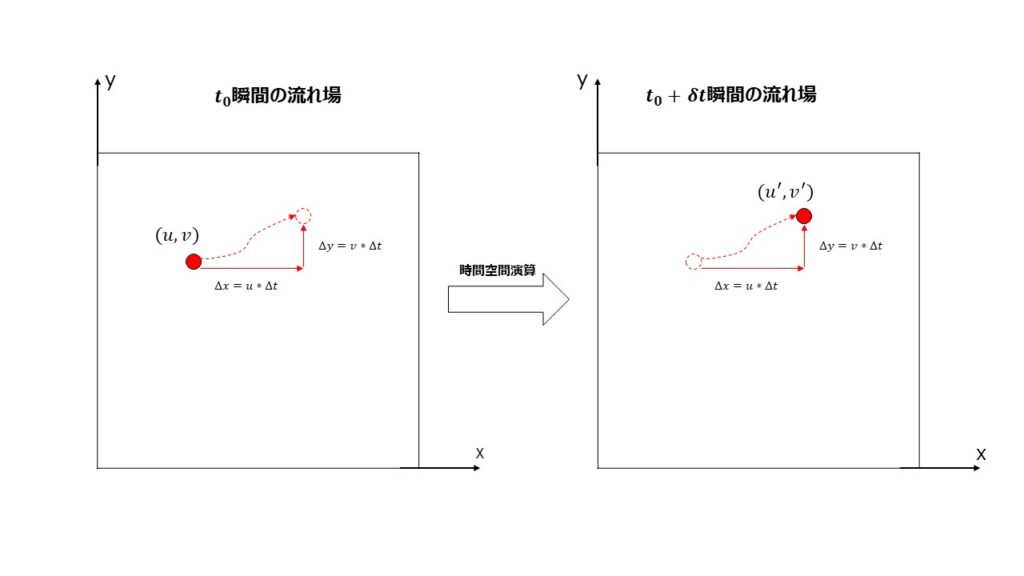
$$du=u^{‘}-u=\frac{\partial u}{\partial t}+\frac{\partial u}{\partial x} \cdot \Delta x+ \frac{\partial u}{\partial y} \cdot \Delta y ~~~~~~~~~~ (1)$$
$$dv=v^{‘}-v=\frac{\partial v}{\partial t}+\frac{\partial v}{\partial x} \cdot \Delta x+ \frac{\partial v}{\partial y} \cdot \Delta y ~~~~~~~~~~ (2 )$$
さらに下記関係があり、
$$\Delta x=u \cdot \Delta t ~~~~~~~~~~ (3)$$
$$ \Delta y=v \cdot \Delta t ~~~~~~~~~~ (4)$$
数式(3)と(4)を数式(1)と(2)に代入すると、下記数式が現れる。
$$\frac{du}{dt}=\frac{\partial u}{\partial t}+u \cdot \frac{\partial u}{\partial x}+ v \cdot \frac{\partial u}{\partial y} ~~~~~~~~~~ (5)$$
$$\frac{dv}{dt}=\frac{\partial v}{\partial t}+v \cdot \frac{\partial v}{\partial x}+ v \cdot \frac{\partial v}{\partial y} ~~~~~~~~~~ (6)$$
数式(5)と(6)をベクトル式に書き換えると、
$$\frac{d \mathbf{u} }{dt} = \frac{\partial \mathbf{u}}{\partial t}+(\mathbf{u} \cdot \nabla ) \mathbf{u} ~~~~~~~~~~ (7) $$
数式(7)の左側は何だろう、風船の加速度だよね。右側は何とナビエストークス方程式の左側とそっくりだ、そうだ、速度の時間偏微分(加速度項)と移流項はここにも表れた。
移流項の物理意味はすなわちオイラー型表現に置かれた流れ場の空間分布による流体に働いている力だ。
要は、流体は自身の速度空間分布によって動かされているね。だから非線形だよね、自分自身が自分に変化を起こしているのだ。ちなみに、「速度時間微分項=0」の流れは定常流れと呼ばれている。「移流項=0」の流れは一様流れと呼ばれている。
もう少しナビエストークス方程式の右側も見てみようとすると、右側第一項は圧力勾配項であり、圧力差によって流体に力を働いていることを表している。右側第二項はラブラシアン演算子が速度場に作用している拡散項(または粘性項)であり、流体の運動を回りに拡散される力を表している。右側第三項は外力項であり、流体に直接に与えている外力だ。例えば、重力、電磁力など。
第一項と第三項を合弁して書いて並び方を変えると、下記のようにナビエストークス方程式は結構伝熱方程式の形に近付ける。唯一、前に紹介した移流項が違うのだ。しかし、このただ一つの移流項の存在によって、流場は本質的に非線形になり、流体の世界は根本的に変わっていた。
$$ -\nu \nabla^2 \mathbf{u}+\frac{\partial \mathbf{u}}{\partial t}+(\mathbf{u} \cdot \nabla ) \mathbf{u} = \frac{\mathbf{F}- \nabla{P} }{\rho}$$
熱には乱れがないが、流体には乱れがユビキタス
温度が空間的に均一で時間的に安定しているものは簡単に作られる。氷、沸かしているお湯、はその代表的な例だ。熱の世界には、原因がなく時間と空間の乱れは見つかっていない。
流体の世界は熱の世界と全く違う、原因がなくても時間と空間の乱れはいつまでも絶えずに起きている。500年前に、レオナルド ダ ヴィンチは水流れの乱れに気づき、高度な絵画技術で乱流を紙に残した。

今では日常生活に起きているほとんどの流体現象は乱流であると確認されている、たとえば、走行中の車周りの流れ、飛行機の流れ、ビル風、蛇口の水流れ、噴水池など、エンジニアリング上では高速カメラ、フローマーカー、PIV技術などによって乱流をリアルに可視化できている。ただ、下図の乱流速度履歴が示したように、いくら過去の速度があっても、次の瞬間の流速は予測できない。これは乱流の予測不可性というもの。任意に二つの時間断面抽出しても、速度変化履歴は重複がない。これは乱流の不重複性というもの。そして、任意時間断面の時間平均値はほぼ変わっていない。
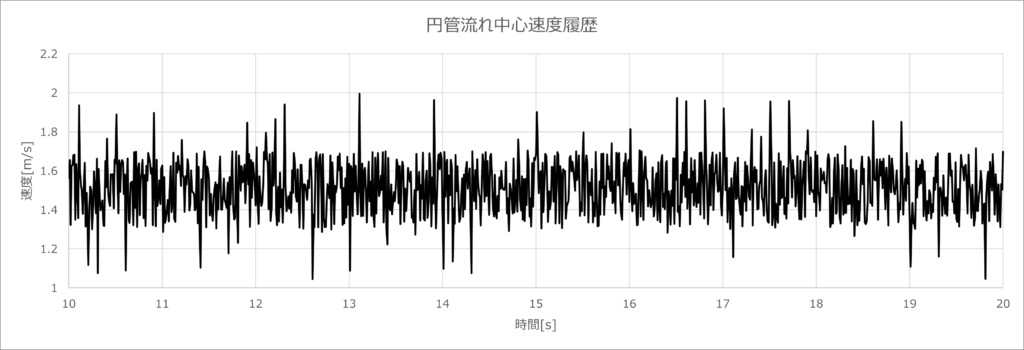
流体のみならず、乱れがこの世界ではユビキタスの者であることは確認されている、例えば、駅での人の流れ、株価の変動、ウイルス感染プロセスなどなども乱れがあると容易に考察されている。しかし、乱れの発生メカニズムについてまだ理論が確立されていなく、どうやって乱れが生まれたかは統一した見解がない。
私見として、
沢山の”自主意識”を持っている個体が集合して相互作用しながら運動していること
は乱れ現象が共通している点だ。
流体も巨視的には一つの連続体となっているが、マイクロ的にはスケールが異なる無数の渦の集合となっています。これらの渦たちは一刻も止まりがなく生成、合体、分裂、消滅している。1個1個の渦はナビエストークス方程式に従って、左側の移流項によって”自主”運動している(慣性)、右側の拡散項によってによって消滅されている。
(provided by
(Provided by Fluid Dynamics Group UPM, with special thanks to Prof. Javier Jimenez)
完全ではないが、Lord Renauldsの乱流試験から、いろんな側面から 少しづつ乱流については理解してきている。乱流もナビエストークス方程式に従っているはずなことは数学上で確認されている
そのために、\( \mathbf{u} \)と \( \mathbf{p} \)を乱れ成分とすると、
$$\mathbf{u}=\mathbf{\bar{u}}+\mathbf{u’}$$
$$\mathbf{p}=\mathbf{\bar{p}}+\mathbf{p’}$$
そして
$$ uv=(\bar{u}+u’) \cdot (\bar{v}+v’) =\bar{uv}+\bar{u} v’+u’ \bar{v}+u’v’$$
u’とv’は微小な乱れ成分のため、時間平均作用すればなくなり、\(\bar{u’}\)と \(\bar{v’}\)とも0になる。
$$\overline{uv}=\overline{ \bar{uv}+\bar{u} v’+u’ \bar{v}+u’v’ }=\overline{ \bar{uv} }+\overline{ \bar{u} v’ }+\overline{ u’ \bar{v} }+\overline{u’v’}= \overline{ uv}+ \bar{u} \bar{v’} + \bar{u’} \bar{v} +\overline{u’v’} =\overline{ uv}+\overline{u’v’} $$
本来のナビエストークス方程式を時間平均作用して、乱流成分を顕在化させると、下記数式に代わる。
$$ \frac{\partial \mathbf{\bar{u}}}{\partial t}+(\mathbf{ \bar{u} } \cdot \nabla ) \mathbf{ \bar{u} } + \color{red}{(\mathbf{ \bar{u’} } \cdot \nabla ) \mathbf{ \bar{u’} }} = -\frac{\nabla{ \bar{P} }}{\rho}+\nu \nabla^2 \mathbf{ \bar{u} }+\frac{\mathbf{F}}{\rho}$$
この前に紹介した移流項から乱流成分の移流項が生まれた、これは完全に未知数(レイノルズ応力)となっており、時間平均のナビエストークス方程式が閉じていなかったことになる。しかも、そのレイノルズ応力は試験でも測定が極めて困難しているため、試験からの物理特性を考察、分析することさえできていない。
そのために、Prantl氏を初めとしてその乱流成分の移流項を既知の変量で表すことを心強く試行錯誤してきました。混合長モデル、k-εモデル、k-ωモデルなどが提案された、20世紀中に計算流体力学(CFD)の基礎を築いた。先人たちの天才的な発想と勇敢な探索に感動している。
熱と流体の最大な違いは流体のほうが移流項と乱流成分が存在していることだ。
続いて、熱と流体の空間発展スピードについて比較してみよう。
まずは、熱側については下記思考試験をやってみてください。
下図のように、最初温度が\(T_{init}\)となっているある塊の上面に温度が \(T_{hot}\)の熱源と接触して、温められるプロセスを考えてみよう。上面以外のすべての面は断熱されていて、熱移動が不可能な境界となっている。 そうすれば、あるタイミングでこの塊は必ず熱源と同一温度になって温度平衡状態になると簡単に想像できるだろう。私達は、その状態にかかる時間を解いてほしい。
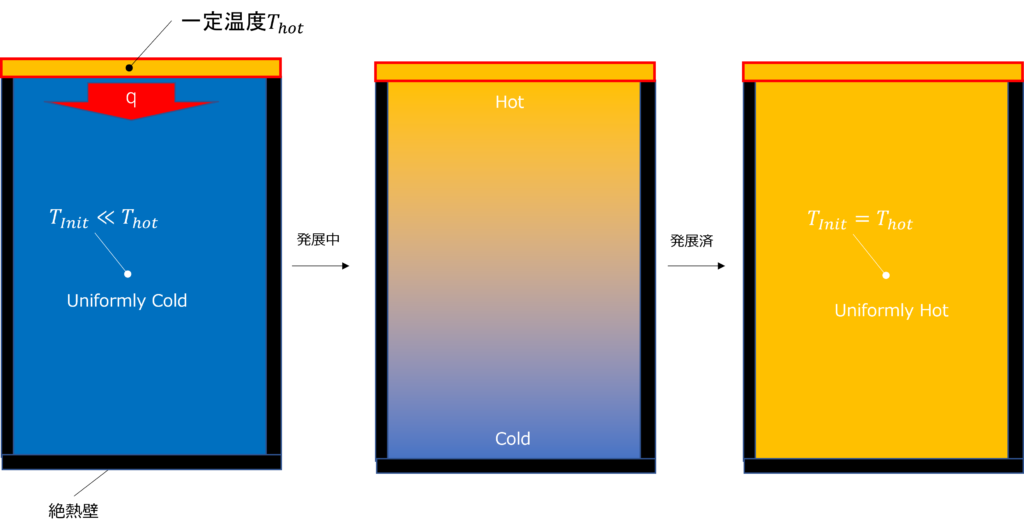
起点はやはり伝熱方程式。ただ、今回は空間的境界条件と時間的初期条件はシンプルなため、塊を点モデルで表現して、3次元の伝熱方程式が1次元に退化させることができる。
$$ m \cdot C_v \frac{dT}{dt}=-C \cdot (T-T_{hot})$$
うち、mは質量、\(C_v\)は比熱、Cは熱伝導係数。
これは常微分方程式であるため、\(T^{`}=T-T_{hot}\)の変換で、下記数式が得られる。
$$ m \cdot C_v \frac{dT^{`}}{dt}=-C \cdot T^{`} $$
少し調整すれば、
$$ \frac{dT^{‘}}{T^{‘}} =-\frac{C}{m \cdot C_v} dt$$
ここで、 \(C=\frac{1}{R}\)で代入して変換すれば、
$$ \frac{dT^{‘}}{T^{‘}} =-\frac{1}{m \cdot C_v \cdot R} dt$$
さらに、 \(m \cdot C_v \cdot R \\)を\tauにまとめて代入すれば、
$$ \frac{dT^{‘}}{T^{‘}} =-\frac{1}{\tau} dt$$
そして、両側積分算子をかけると、
$$\int\limits_{ T^{‘}_0 }^{T^{‘}} \frac{dT^{‘}}{T^{‘}}=-\int\limits_{t_0}^{t} \frac{1}{\tau} dt$$
そして、
$$ \ln{\frac{ T^{‘} }{ T^{‘}_0 }}=-\frac{t-t_0}{\tau}$$
そして、
$$T^{‘}= T^{‘}_0 \cdot e^{ -\frac{t-t_0}{\tau} }$$
最後に、 \(T^{`}=T-T_{hot} \)を戻してら、
$$T= T_{hot} +(T_{init}-T_{hot}) \cdot e^{ -\frac{t-t_0}{\tau} }$$
ここまで導いたら、塊の温度変化が指数に従って\(T_{init}\)から \(T_{hot}\)に変化し 、時間定数\(\tau\)に変化スピードに依存していることが分かる。ざっくりでは、 \(3\tau\)程度の時間で温度場が発展完了と近くなる。
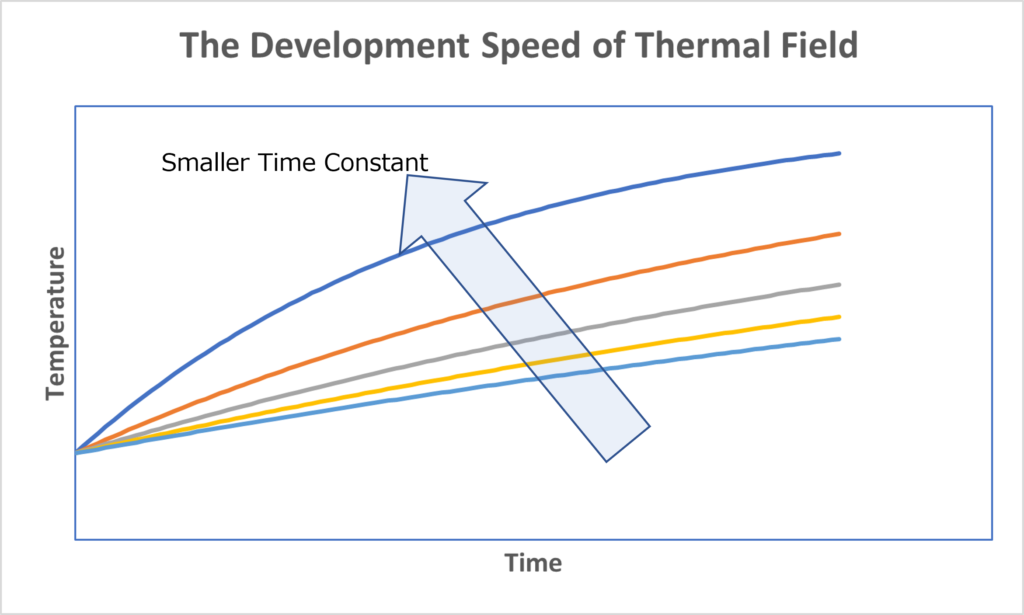
実際の時間定数はどうなんだろう、電気自動車の電池パックの熱容量は200,000~300,000\(\frac{J}{K}\)程度で、時定数は12時間程度、成人の熱容量は210,000 \(\frac{J}{K}\) 程度、時定数的には7時間程度。大体、日常生活使っている製品の熱時定数の数時間程度のものが多い。
一方、流体の特徴時間は代表速度と代表長さに決まれており、
$$\delta t=\frac{L}{U}$$
自動車の例とすれば、車速40kphでも2mの代表長さでも特徴時間はただ0.2sであり、乗客室でもHVAC風速が2.5m/sとすると、特徴時間が1s前後になる。きわめて発展が遅い自然対流以外に、扇風機や走行風などを利用して冷却しているシーンにおいては、流れ場の発展時間数十秒以内。
従って、 流体は熱より空間発展スピードが速いシナリオがよく見られる。
長く説明してきが、
熱と流体は本質的に違うものとなっているため、分けて解析することが当たり前のこと。
熱と流体を無理やり一つのモデルで解析すること実体ができるが、解析負担が膨大になることを招き、せいぜい定常解析しかできなくて、過渡解析が非現実な時間がかかる壁にぶつかる。
今回は熱と流体を分けて解析すべきことを説明しました、次回は熱解析と流体解析の連成手法について語りたいと思っております。
ここまで読んでいただき、ありがとうございます。よろしくお願いします。